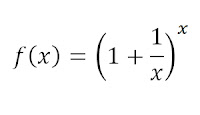Bon viatge!!!!!!!!!

Terminó esta fiesta y los alumnos de 4º inician su andadura por tierras catalanas en su viaje de fin de curso. Espero que esta fiesta haya sido entretenida y que el próximo curso quieran volver a ser invitados. Ahora nos queda a las profes recoger y decorar este blog con sus proyectos finales. Hasta la vuelta....

Sólo para los invitados

Ya todos los invitados a esta fiesta conocen a su protagonista. Con mayor o menor "aproximación" (eso depende de quien haya sido nuestra pareja de baile en la fiesta) todos hemos llegado al conocimiento de este número que tanto maravilla a muchos matemáticos (y a aspirantes a serlo). Aquí va mi regalo a la fiesta (quizás alguno de ustedes quiera utilizarlo en esos trabajillos que están elaborando para sus profesoras).

Dedicatoria especial

A todos aquellos que vieron al número e "colgado" de un cable de la luz:

Y a los que hacen uso de su última titulación

¿Cómo "ver" el valor de e? Aproximación gráfica

En Recursos, tienes una explicación del uso de Geogebra para representar funciones y, de manera específica, "caminar por ella", observando las coordenadas de los puntos sobre los que nos movemos.

Hay una función que nos permite "acercarnos" al valor de e si nos movemos "mucho" hacia la derecha. Es, decir, que si tomas valores de x cada vez más grandes, el valor de su imagen, f(x) se va "acercando" a ese número extraño llamado e.

Tu tarea ahora consiste en construir la función que aparece aquí, en Geogebra, obtener su gráfica, moverte por ella y, ... obtener una captura de pantalla donde se observe esa representación gráfica que has obtenido, así como varios puntos sobre los que te has situado y que ha dado lugar a "esa aproximación" obtenida de e.

• La entrega de esta parte de la tarea será a través del correo electrónico (alumnos de 4ºA) o EVAGD (alumnos de 4ºB)

En ambos casos, un documento de office, openoffice o similar (imagen + texto explicativo)

• Plazo de presentación: 24 de mayo (hasta las 23:55 horas)

Mas por menos

El siguiente video hace un recorrido por la historia del número e y algunas de sus utilidades. Pertenece a la serie de TVE, Mas por menos:

Prepara calculadora y lápiz, junto con las siguientes fórmulas, para resolver el siguiente cuestionario:

La hora de los irracionales

Y también la hora de trabajar con imágenes. Este reloj es muy especial: puedes comprobar cómo las horas no son siempre racionales (ya quisieramos).... pero no, no vamos a hablar de horas ni de plazos. Vamos a hablar de imágenes del número e. Cada uno de ustedes deben regalarnos una imagen comentada que deberán subir al album compartido para tal efecto. Veremos cuál es la más original de todas.

Una selección de números irracionales situados en un reloj que, naturalmente no marca las horas ‘exactas’ sino otras muy especiales, con infinitos decimales. Por ejemplo el nº e está un poco antes del 3 y el nº π un poco después. Por cierto que no se llaman números irracionales porque no sean razonables, se razonan muy bien, sino porque no se pueden poner como una razón (n/m). Los pitagóricos les llamaron incomensurables, porque rompían sus ideas sobre la medida de los números, pero desde hace siglos son números bien definidos y controlados, aunque siguen siendo incómodos para los estudiantes.  Foto trendencias vía @MisVoces

FUENTE: FOTOMAT

El album se va actualizando con sus imágenes:

Leonhard Euler, el genio de las matemáticas que inunda Internet

El buscador más famoso del mundo celebra el 306º aniversario del nacimiento del genial matemático y físico suizo.

Leonhard Euler fue un hombre con un recorrido vital apasionante, digno de figurar en las escuelas de todo el mundo. Adentrémonos en su obra y empecemos desde su nacimiento. Leonhard Euler vio la luz como hijo de un pastor calivinista, Paul Euler, y de Marguerite Brucker. Su infancia la desarrolló en la ciudad de Riehen, hacia donde emigró su familia procedentes de su Basilea natal. Precisamente fueron las amistades de sus padres las que contribuyeron de forma decisiva en su inclinación científica. No en vano, frecuentaba a la familia Bernoulli, en cuyo núcleo destacaba Johann Bernoulli, por entonces considerado la eminencia matemática en toda Europa. De forma casi inmediata, se convirtió en la principal influencia de Leonhard Euler.

Leonhard Euler sin embargo se matriculó a los 13 años en la Universidad de la que fuera su primera ciudad: Basilea. A los 16, en 1723, ya recibió el título de maestro de Filosofía gracias a una disertación comparativa entre René Descartes e Isaac Newton. Ahí es nada. Mientras tanto, Bernoulli no descuidaba su formación. Leonhard Euler, además, tenía tiempo para el estudio del griego y el hebreo y, por otro lado, adentrarse en el mundo de la teología. Pero fue el propio Bernoulli el que decidió que su campo debía ser las Matemáticas. En 1726 puso punto y final a su doctorado, construyendo una tesis sobre la propagación del sonido, a la que llamó 'De Sono5'. Por si fuera poco, un año más tarde participó en el concurso organizado por la Academia de las Ciencias francesa que consistía en dar con la mejor forma posible de situar el mástil en un buque. Quedó segundo. Más tarde, Leonhard Euler lograría el primer puesto doce veces.

Leonhard Euler asumió el puesto en el departamento de matemáticas y física de la Academia de las ciencias de Rusia en San Petersburgo que había dejado vacante Nicolás, el hijo de Johann Bernoulli, tras su muerte. A su llegada a Rusia se aclimató como uno más. Aprendió el idioma y se hizo a la vida allí. En 1731, tras varios problemas con el suministro de subvenciones a la institución, Leonhard Eulerocupoó la dirección del departamento de Matemáticas. Tres años después, nuestro protagonista se casó con Katharina Gsell, hija de un pintor de la Academia. A lo largo de su vida en común llegaron a concebir un total de trece hijos. Pero, por desgracia, solo sobrevivieron cinco de ellos en la edad adulta.

Leonhard Euler llegó en 1741 a la Academia de Berlín por petición expresa de Federico II el Grande, rey de Prusia. Allí vivió 25 años, tiempo suficiente para producir 380 artículos. En su época alemana concibió además dos de sus obras monumentales: la 'Introductio in analysin infinitorum', acerca de las funciones matemáticas, y la 'Institutiones calculi differentialis', que trató sobre el cálculo diferencial.Leonhard Euler también editó sus 'Cartas de Euler', volumen escrito que versaba temas de Filosofía Natural y que dirigía a una princesa alemana. El éxito fue inmediato y bestial. Pese a su prestigio, abandonó la ciudad tras una disputa con Federico, el que había sido su protector. También contribuyeron sus desavenencias con Voltaire, excepcionalmente considerado en la Corte.

Leonhard Euler sufrió a lo largo de su vida un deterioro de la visión que le condicionó ciertos hábitos. En 1738 ya se había quedado ciego del ojo derecho. En años sucesivos, además, padeció de cataratas en el otro ojo e incluso sufrió una ceguera total durante varias semanas. Estos inconvenientes no influyeron en el poder de su mente. De ahí que, por ejemplo, pudiera recitar la Eneida de Virgilio desde la primera palabra hasta la última. Para más inri, era capaz de recordar las fórmulas de la triognometría y todas las seis primeras potencias de los 100 primeros números primos. A este respecto cabe recordar la cita delmatemático francés François Arago "Leonhard Euler calculaba sin esfuerzo aparente, como los hombres respiran, o como las águilas se sostienen en el aire".

Leonhard Euler regresó a Rusia en pleno apogeo de Catalina la Grande. Corría 1766 y ya formaba parte de nuevo de la Academia de San Petersburgo. Ahí trabajaría hasta el final de sus días. Fue una época dura, como muestra el incendio de 1771 que le privó de su casa. Dos años después, Leonhard Euler se quedó sin su mujer, que falleció con solo 40 años. En 1743 volvería a contraer matrimonio. 40 años después murió en la ciudad rusa después de ser víctima de un ataque cerebrovascular. Sus resto fueron enterrados en el Cementerio Luterano de Vasilievsky, pero más tarde se llevaron al Monasterio de Alejandro Nevski. Leonhard Euler recibe hoy en día el reocnocimiento que merece una vida dedicada a la investigación bajo el prisma de una mente brillante e inigualable. Así repasa Youtube su vida:

Leonhard Euler no dejó de tocar todos los ámbitos de las matemáticas: desde la geometría hastala trigonometría, pasando por el cálculo, el álgebra, la teoría de números, la física continua, la teoría lunar y más ámbitos de la física. Prolífico donde los haya Leonhard Euler produjo a un ritmo de 800 páginas anuales entre 1727 y 1783. Opera Omnia es la obra que recopila sus trabajos. Comenzó a elaborarse en 1911 y por el momento la forman 76 piezas. Como curiosidad, se tiene la creencia de que fue él mismo el que posiiblitó el nacimiento del Sudoku al establecer ciertos hábitos en el cálculo de probabilidades. Leonhard Euler introdujo en el círculo matemático la fundión matemática: fue pionero al escribir f(x) para hacer referencia a la función f aplicada sobre el argumento x. Además, inventó la letra 'e' como base del logaritmo natural o neperiano, la letra griega 'Σ' a modo de símbolo de los sumatorios y la letra 'i' con el opbjetivo de hacer referencia a la unidad imaginaria.

Leonhard Euler tuvo tiempo para abarcar diferentes campos de la ciencia. Más allá de la mencionada teoría de los números, por la que estableció la conexión entre la función zeta de Riemann y los números primos, diseño la Teoría de grafos y geometría, se introdujo en la matemática aplicada, la física y astronomía, la lógica, la arquitectura y la ingenieria. Sin duda, Leonhard Euler fue una figura genial para su tiempo, pionera y moderna, padre de muchos fundamentos todavía hoy vigentes. Leonhard Euler fue un personaje casi inabarcable y digno de todas la admiración posible. Por eso resultad ideal traer a colación su nombre en un día como hoy. Disfrutemos de su obra y descubramos todo de lo que fue capaz.

FUENTE:  IDEAL.ES

Bueno, ahora te toca a tí demostrar que eres un genio de la lectura. El reto de hoy es que me elijas cinco momentos en la vida de Euler que tú creas que son los más importantes en su biografía.